Projections

Section author: Luke Frisken <l.frisken@gmail.com>

Introduction

Projection classes derived from the Projection class are used to represent a type of map projection. These are important to this project because projections allow the 3d spherical coordinates to be transformed into flat representation which is easier to work on.

Different types of projections have different properties making them more or less suitable depending on the application. For our case, it is important that the projection be as close to Euclidean space as possible in the area it is being used. This will allow us to assume such, and simplify our calculations with minimal effect on the accuracy. Performance, and ease of implementation are also factors.

These projections must be capable of transforming a GeographicCoordinate or SphericalVelocity into a vector position within its own coordinate system. This is achieved through the implementation of the methods:

• Projection#transformPositionTo
• Projection#tranformVelocityTo

Positions in the projection’s coordinate system are transformed back into GeographicCoordinate or SphericalVelocity through the implementation of the methods:

• Projection#transformPositionFrom
• Projection#transformVelocityFrom

Gnomonic Projection

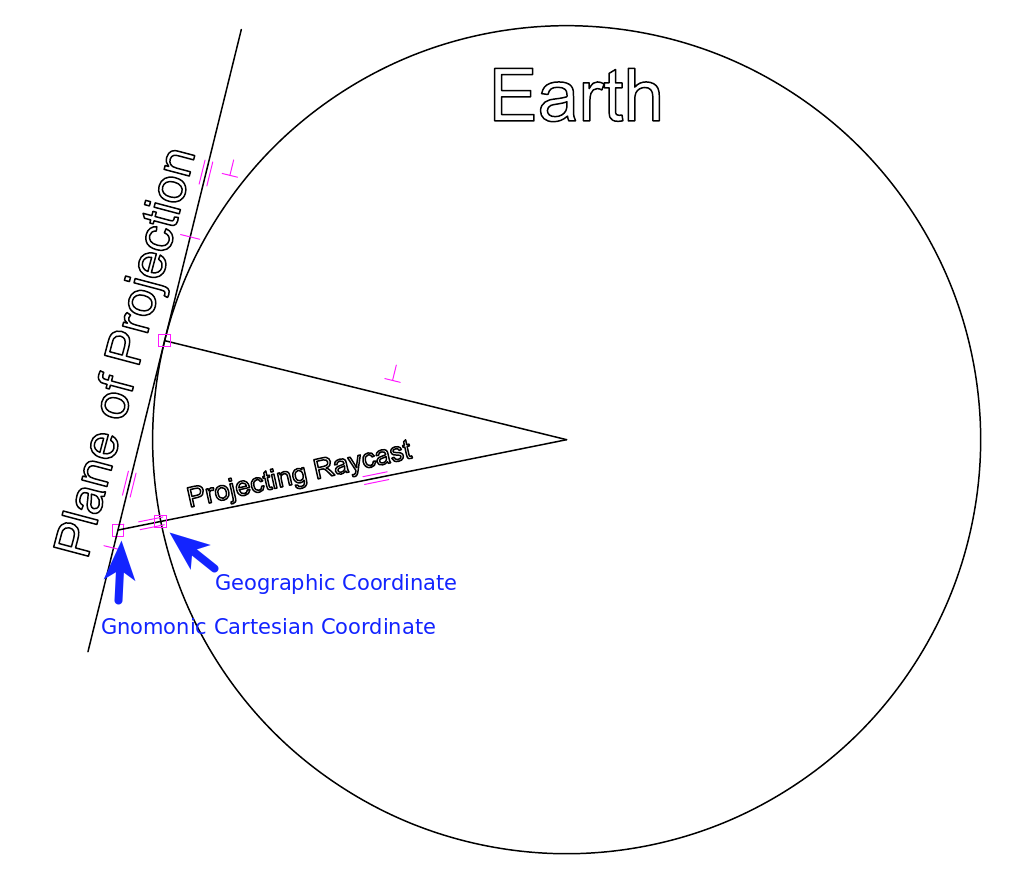
Gnomonic Projection

Gnomonic projection is formed by projecting points on the sphere of the earth onto a plane, which is located/touching the earth at a certain point known as the Reference Position within this project. By convention in this project, this plane has its own coordinate system, with the y axis aligned to the north direction. The points are projected using a ray which originates from the center of the earth.

Ensuring that the Reference Position is as close as possible to the points which are to be projected and worked upon in the projection enables the simplifying assumption that this is Euclidean space to have minimal impact on the accuracy of the calculations.

Gnomonic projection capabilities are implmented twice within this project. The first (and most important) is in the GnomonicProjection class.

The second place is in the display.DisplayApplication, which uses Gnomonic projection to display the map in OpenGL by placing the camera at the center of the planet, and rendering the planet and elements on the map in cartesian space. As OpenGL transforms the elements on the map into 2d screen space, this is implicitely undergoing a Gnomonic projection.

Stereographic Projection

The stereographic projection has yet to be implemented within the project. Many commercial displays use this projection but the implmementation is slightly more complicated, an it is not yet certain whether it will be of any significant benefit.